Exploring The Laplace Transform: A Powerful Tool In Mathematics And Engineering

Exploring the Laplace Transform: A Powerful Tool in Mathematics and Engineering

Related Articles: Exploring the Laplace Transform: A Powerful Tool in Mathematics and Engineering

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Exploring the Laplace Transform: A Powerful Tool in Mathematics and Engineering. Let’s weave interesting information and offer fresh perspectives to the readers.

Exploring the Laplace Transform: A Powerful Tool in Mathematics and Engineering

The Laplace transform, a mathematical tool developed by Pierre-Simon Laplace in the late 18th century, provides a powerful framework for analyzing and solving differential equations. Its significance extends beyond theoretical mathematics, finding crucial applications in diverse fields such as electrical engineering, control systems, signal processing, and physics. This article delves into the intricacies of the Laplace transform, elucidating its fundamental principles, practical applications, and inherent benefits.

Understanding the Laplace Transform

The Laplace transform essentially translates a function of time, often representing a physical system’s behavior, into a function of a complex variable ‘s’. This transformation allows for a shift from the time domain to the frequency domain, offering a different perspective on the system’s dynamics.

Key Features of the Laplace Transform:

• Conversion of Differential Equations: The Laplace transform converts differential equations into algebraic equations, simplifying their solution process. This transformation eliminates the need to directly deal with derivatives, simplifying the mathematical operations involved.
• Frequency Domain Analysis: The Laplace transform provides insights into the frequency response of a system, revealing how it reacts to different input frequencies. This analysis is crucial for understanding the stability and performance of systems in various engineering applications.
• System Modeling: The Laplace transform facilitates the representation of complex systems using a concise mathematical framework. This representation allows for a more straightforward analysis of system behavior and prediction of its response to various inputs.
• Solving Initial Value Problems: The Laplace transform is particularly effective in solving initial value problems, which are common in engineering and physics. It allows for the direct incorporation of initial conditions into the solution process, simplifying the derivation of system behavior.

Applications of the Laplace Transform:

The Laplace transform finds widespread application in various fields, including:

• Electrical Engineering: Analyzing circuit behavior, solving for currents and voltages in complex circuits, designing filters, and understanding the stability of electrical systems.
• Control Systems: Designing controllers for feedback systems, analyzing system stability, and optimizing system performance.
• Signal Processing: Analyzing and filtering signals, identifying and removing noise, and compressing data.
• Mechanical Engineering: Modeling and analyzing mechanical systems, solving for vibration and dynamic responses, and designing control systems for robotic applications.
• Physics: Solving problems related to heat transfer, wave propagation, and fluid dynamics.

Benefits of Using the Laplace Transform:

• Simplicity and Efficiency: The Laplace transform simplifies complex mathematical operations, making the analysis of systems more efficient.
• Frequency Domain Insights: The transform allows for a clear understanding of system behavior in the frequency domain, providing valuable information for design and optimization.
• System Modeling and Analysis: The Laplace transform offers a powerful tool for modeling and analyzing complex systems, facilitating a comprehensive understanding of their behavior.
• Solving Initial Value Problems: The transform simplifies the solution of initial value problems, making it a valuable tool for solving real-world engineering and physics problems.

Frequently Asked Questions (FAQs):

Q: What is the difference between the Laplace transform and the Fourier transform?

A: Both transforms are powerful tools for analyzing signals and systems. However, the Laplace transform is more general than the Fourier transform, allowing for the analysis of signals with complex frequencies and incorporating initial conditions. The Fourier transform focuses on analyzing signals in the frequency domain, while the Laplace transform encompasses both time and frequency domains.

Q: How do I calculate the Laplace transform of a function?

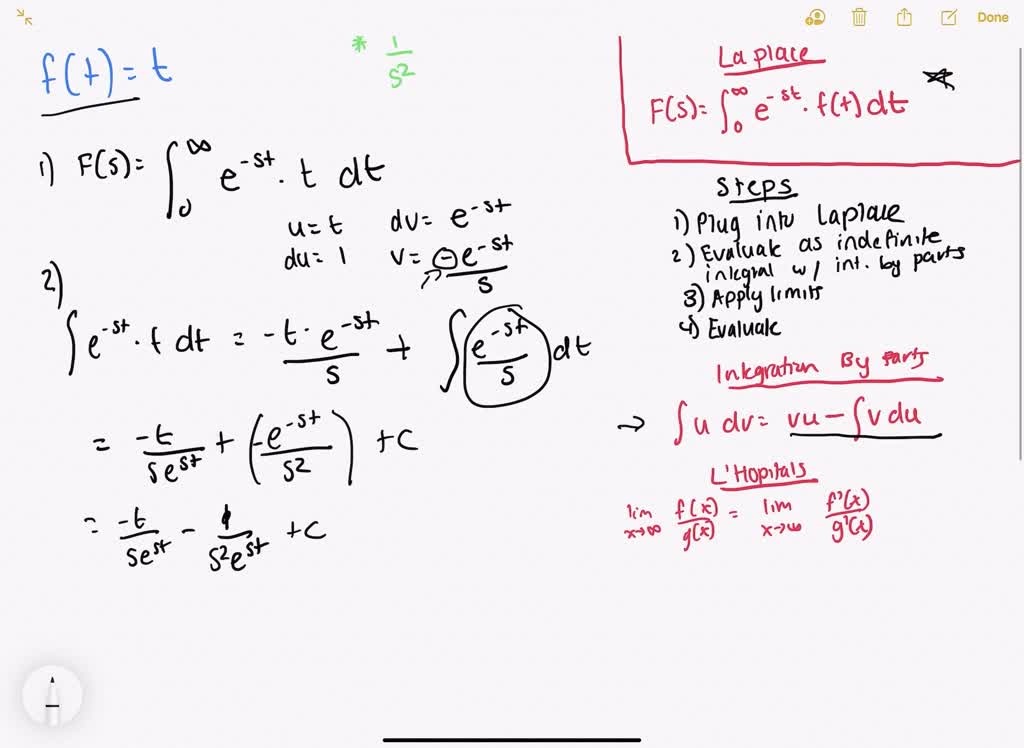
A: The Laplace transform of a function f(t) is defined as:

F(s) = ∫[0, ∞] e^(-st) f(t) dt

where ‘s’ is a complex variable. The integral is calculated over the time domain, resulting in a function of ‘s’ in the frequency domain.

Q: What are some limitations of the Laplace transform?

A: While the Laplace transform is a powerful tool, it does have limitations. For instance, it is not always possible to find the Laplace transform of a function, and some functions may have complex Laplace transforms that are difficult to interpret. Additionally, the transform may not be suitable for analyzing non-linear systems or systems with time-varying parameters.

Tips for Utilizing the Laplace Transform:

• Understanding the Basic Concepts: Familiarize yourself with the definition of the Laplace transform, its properties, and common transform pairs.
• Practicing Problem Solving: Solve various problems involving differential equations, system analysis, and initial value problems using the Laplace transform.
• Utilizing Tables and Resources: Utilize readily available tables of Laplace transforms and other resources to simplify calculations and enhance understanding.
• Understanding the Limitations: Be aware of the limitations of the Laplace transform and consider alternative methods when necessary.

Conclusion:

The Laplace transform is a fundamental tool in mathematics and engineering, providing a powerful framework for analyzing and solving problems related to differential equations, system behavior, and signal processing. Its ability to simplify complex mathematical operations, offer insights into the frequency domain, and effectively model and analyze systems makes it an indispensable tool in various fields. By understanding the principles, applications, and limitations of the Laplace transform, engineers and scientists can effectively leverage its capabilities to solve complex problems and advance technological development.

Closure

Thus, we hope this article has provided valuable insights into Exploring the Laplace Transform: A Powerful Tool in Mathematics and Engineering. We thank you for taking the time to read this article. See you in our next article!